カルマンフィルタを用いたセンサフュージョン(2)
前回の内容
前回は図1に示す対向二輪型ロボットの位置及び姿勢を推定するために、カルマンフィルタを用いることを考え、「姿勢」についての状態方程式と観測方程式を考えました。
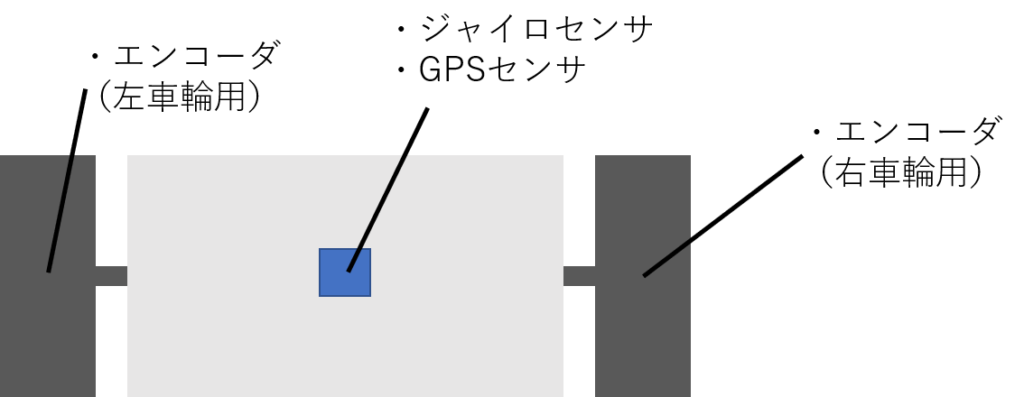
今回は対向二輪型ロボットの「位置」に関する状態方程式と観測方程式を考えようと思います。
位置推定用の状態方程式と観測方程式の導出
前回と同様にまずは注目する状態(今回の場合位置)に関する数理モデルの式を導出します。
位置に関する式を次式に示します。
$$x_{k + 1} = x_k + v_{k_x} \delta t \tag{7}$$
$$y_{k + 1} = y_k + v_{k_y} \delta t \tag{8}$$
ここで、$x$、$y$はロボットの位置を、$v_x$、$v_y$はロボットの速度、$\delta t$はマイコンの制御周期を表しています。
次に式$(7)$と式$(8)$を用いて、状態方程式を導出します。
$$\begin{pmatrix}
x_{k + 1} \\
y_{k + 1}
\end{pmatrix}
=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}
\begin{pmatrix}
x_k \\
y_k
\end{pmatrix}
+
\delta t
\begin{pmatrix}
v_x \\
v_y
\end{pmatrix}
\tag{11}
$$
ここで
$$\boldsymbol{x_k} =
\begin{pmatrix}
x_k \\
y_k
\end{pmatrix}
、
A_{xy} =
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}
、
B_{xy} =
\delta t
、
\boldsymbol{u_k} =
\begin{pmatrix}
v_x \\
v_y
\end{pmatrix}
$$
とします。
また、$x_k$、$y_K$はGPSセンサで直接観測できますが、観測誤差$w$を含むため観測方程式は以下のようになります。
$$\begin{pmatrix}
x_k + w \\
y_k + w
\end{pmatrix}
=
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}
\begin{pmatrix}
x_k \\
y_k
\end{pmatrix}
+
\begin{pmatrix}
w \\
w
\end{pmatrix}
\tag{12}
$$
ここで
$$\boldsymbol{y_k} =
\begin{pmatrix}
x_k + w \\
y_k + w
\end{pmatrix}
、
C_{xy} =
\begin{pmatrix}
1 & 0 \\
0 & 1
\end{pmatrix}
、
\boldsymbol{w_k} =
\begin{pmatrix}
w \\
w
\end{pmatrix}
$$
とします。ここで、GPSセンサは$x$、$y$方向で同様の誤差$w$が生じるとします。
位置推定用のカルマンフィルタ
カルマンフィルタを用いて位置を推定する手順は、前回の姿勢を推定する流れと同様になります。
位置推定用にカルマンゲインと共分散行列を導出し、$\boldsymbol{x}$の最大事後確率を求めます。その後、数理モデルを用いて次ステップ$(k+1)$の状態予測を行います。
以上の流れを繰り返すことで、各ステップにおけるロボットの位置を推定することが出来ます。
まとめ
今回は位置推定用の状態方程式と観測方程式を考えました。前回姿勢を推定する方法は考えたので、これでカルマンフィルタによるセンサフュージョンによってロボットの状態(位置、姿勢)推定が可能となります。
次回は実際にシミュレーションを行って、それぞれのセンサ値から推定した状態と、カルマンフィルタによるセンサフュージョンで推定した状態を比較しようと思います。


