カルマンフィルタを用いたセンサフュージョン(1)
最近「トランジスタ技術2019年7月号」を読んで、カルマンフィルタを学んだので例題を含めてセンサフュージョンについて考えようと思います。
カルマンフィルタとは
カルマンフィルタとは、現在の状態を推定する手法です。「1ステップ過去における状態の推定値」と「現在の測定値」を用いて、「現在の状態」を推定します。
ここではセンサフュージョンを行う際にカルマンフィルタをどのように用いればよいかを説明してきます。カルマンフィルタの理論については「トランジスタ技術2019年7月号」やインターネットを参考にしてください。
例題
図1のような対向二輪ロボットの位置と姿勢を推定することを考えます。
ロボットの車輪にはエンコーダがとりつけられており、車輪の回転角度が求められるものとします。またロボットの機体にはジャイロセンサとGPSセンサが取り付けられており、ロボットの角速度と大まかな位置(誤差1m程度)が計測できることとします。
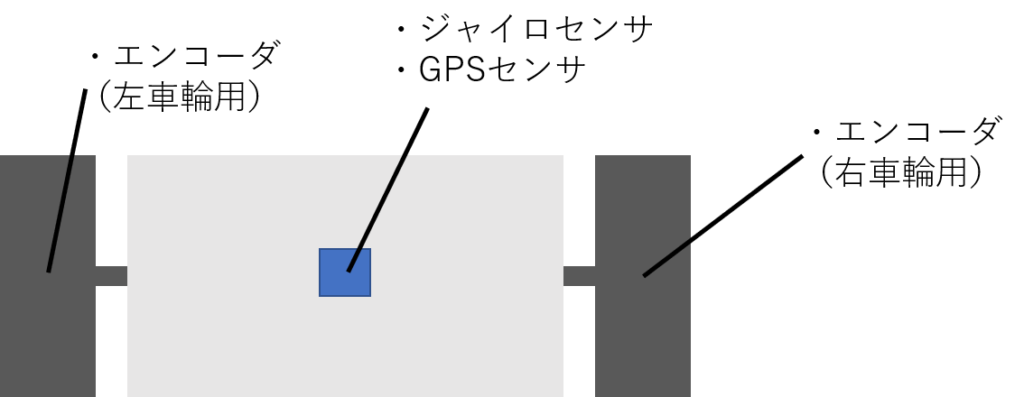
またロボットが走行する地面は、平たんではなく細かな凹凸が存在するとして、車輪と地面の間にはランダムな滑りが生じるものとします。
エンコーダについて
エンコーダで車輪の回転角度を計測することで、ロボットの位置および姿勢を求めることができます。
まず、ロボットの速度を$v$、左右の車輪の速度を$v_l, v_r$とします。ロボットは回転中心$O$を中心にして回転半径$r$、角速度$\omega$で旋回しているとします(図2)。
また、左右の車輪間の距離(トレッド長)を$T$とします。
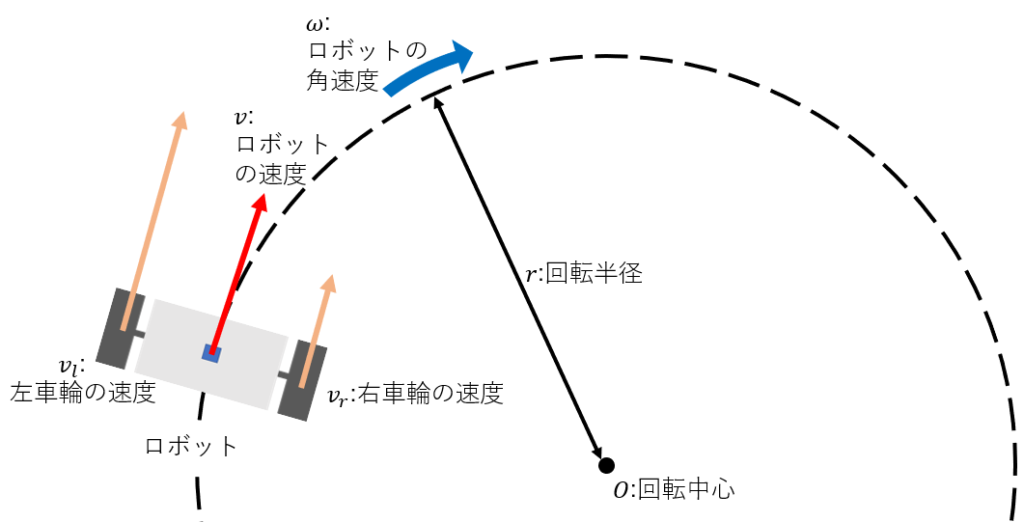
ここで$v = r \omega$より、
$$v_l = (r + T/2) \omega \tag{1}$$
$$v_r = (r - T/2) \omega \tag{2}$$
式$(1)+$式$(2)$より、
$$v_l + v_r = 2r \omega$$
$$r \omega = (v_l + v_r)/2$$
$$v = (v_l + v_r)/2 \tag{3}$$
式$(3)$より$v_l$および$v_r$が分かれば、ロボットの速度を求めることができます。また$v_l$および$v_r$は、制御周期当たりのエンコーダによる左右の車輪の回転角から求めることができます。
一方で式$(1)-$式$(2)$より、
$$v_l - v_r = T \omega$$
$$\omega = (v_l - v_r) / T \tag{4}$$
式$(4)$より$v_l$および$v_r$が分かれば、ロボットの速度と同様にロボットの角速度も求めることができます。
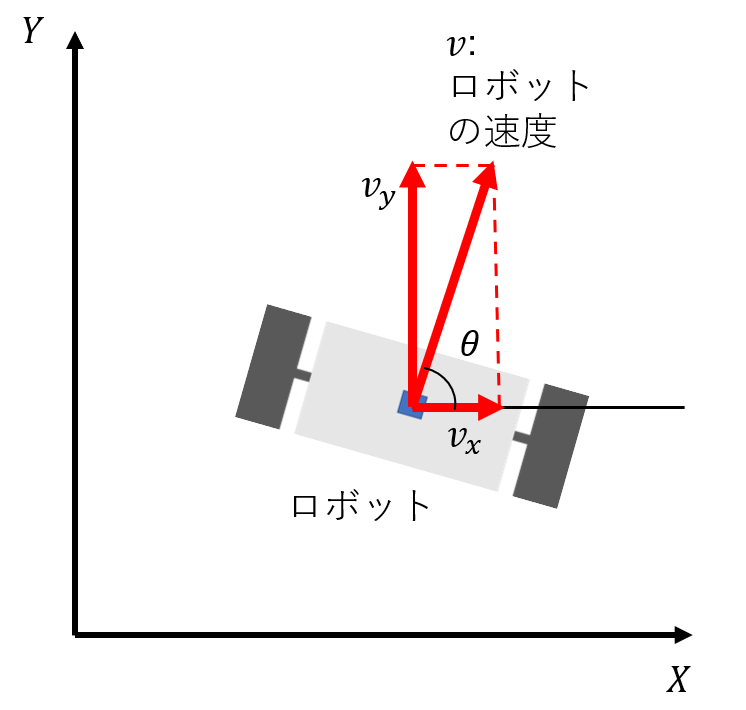
そしてロボットの速度と角速度が分かれば、ステップ$k$におけるロボットの位置$(x_k, y_k)$と姿勢$(\theta_k)$を式$(5)~(7)$のように求めることができます。
$$\theta_k = \theta_{k-1} + \omega_{k-1} \delta t \tag{5}$$
$$x_k = x_{k-1} + v_{k-1} \cos \theta_{k-1} \delta t \tag{6}$$
$$y_k = y_{k-1} + v_{k-1} \sin \theta_{k-1} \delta t \tag{7}$$
ジャイロセンサについて
エンコーダを用いて、式$(4)$のように左右車輪の速度を用いて角速度を計算する場合、車輪と地面に滑りが生じていると、求めた姿勢と実際のロボットの姿勢にずれが生じてしまいます。
そこでジャイロセンサを用いてロボットの角速度$(\omega)$を実際に計測すれば、その角速度を用いて式$(5)$のように姿勢を求めることができます。
ただし、ジャイロセンサの計測値にはオフセット電圧とドリフト電圧が含まれてしまうため、長時間計測していると誤差が大きくなるという短所があります。
GPSセンサについて
ジャイロセンサでロボットの姿勢が求められても、車輪と地面に滑りが生じてしまう場合、エンコーダでは正確な位置を計算することができません。そこでGPSセンサを用いて位置情報を計測することを考えます。
GPSセンサを用いて位置情報を計測する場合、滑りが生じていてもロボットの位置$(x_k, y_k)$を計測することができますが、その位置情報には2mほどの誤差が生じてしまいます(簡単に購入できる市販のセンサの場合)。よってロボットが長距離移動した場合、大まかな位置を計測することはできますが、細かい移動を正確にとらえることはできません。
またGPSセンサの出力は通常1秒ごととなるため、素早い動きは計測できません。
カルマンフィルタの導入
各センサについて、それぞれの特徴を以下にまとめます。
エンコーダ:
- 車輪の回転角度を計測する。
- 左右のエンコーダによる計測値を合わせることによって、ロボットの位置と姿勢を求めることができる。
- 車輪と地面に滑りが生じていた場合、位置および姿勢に誤差が生じる。
ジャイロセンサ:
- ロボットの角速度を計測する。
- 車輪と地面に滑りが生じていたとしても、滑った結果どのくらいの角速度になったかを計測することができる。
- オフセット電圧とドリフト電圧が生じるため、長時間計測していると姿勢の誤差が大きくなる。
GPSセンサ:
- 衛星情報を用いてロボットの位置を計測する。
- 車輪と地面に滑りが生じていたとしても、滑った結果どの位置にいるかを計測することができる。
- 市販のものでは誤差が2mほど発生するものもあるため、細かい移動を計測することができない。
- 通常1秒ごとの受信となるため、素早い挙動を計測することができない。
それぞれのセンサで長所と短所があるため、各センサの出力値を組み合わせて、ロボットの正確な位置と姿勢を求めることを考えます。これをセンサフュージョンと言います。
センサフュージョンの一つの方法としてカルマンフィルタがあります。今回はロボットの正確な位置と姿勢を求めたいので、位置と姿勢用に2つのカルマンフィルタを用いることとします。データ処理の流れを図4に示します。

まずジャイロセンサおよびエンコーダで角速度を測定し、カルマンフィルタによって最も確からしい姿勢を推定します。
ロボットの位置情報については、ロボットの姿勢とエンコーダの出力を合わせて求められた位置情報とGPSセンサの出力値を用いて、カルマンフィルタによって最も確からしい位置を推定します。
このように2つのカルマンフィルタを用いてロボットの姿勢と位置情報を求めることができます。
姿勢推定用の状態方程式と観測方程式の導出
カルマンフィルタでは、「過去の推定値から数理モデルを用いて推測される状態」と「各センサの現在の計測値」を用いて現在の状態を推定します。
まずは注目する状態(今回の場合角度や角速度)に関する数理モデルの式を導出します。
角度と角速度に関する式を次式に示します。ただしここで$\omega_{offset}$はジャイロセンサのオフセット電圧によって計算された角速度とします。
$$\theta_{k + 1} = \theta_k + (\omega_k - \omega_{offset})\delta t \tag{7}$$
またジャイロセンサのオフセット電圧は、時間に依存せず不変であるとします。
$$\omega_{offset}(k+1) = \omega_{offset}(k) \tag{8}$$
次に状態方程式と観測方程式について考えます。
状態方程式と観測方程式の一般式は式$(9)$および式$(10)$となっています。
$$\boldsymbol{x_{k + 1}} = A \boldsymbol{x_k} + B \boldsymbol{u_k} \tag{9}$$
$$\boldsymbol{y_k} = C \boldsymbol{x_k} + \boldsymbol{w_k} \tag{10}$$
ここで$\boldsymbol{x_k}$はシステムの状態、$\boldsymbol{y_k}$は観測できる値、$\boldsymbol{w_k}$は観測雑音(センサで観測した際に含まれるノイズ)、$A、B、C$は係数行列を表しています。
次に式$(7)$と式$(8)$を用いて、状態方程式を導出します。
$$\begin{pmatrix}
\theta_{k + 1} \\
\omega_{offset}
\end{pmatrix}
=
\begin{pmatrix}
1 & -\delta t \\
0 & 1
\end{pmatrix}
\begin{pmatrix}
\theta_k \\
\omega_{offset}
\end{pmatrix}
+
\begin{pmatrix}
\delta t \\
0
\end{pmatrix}
\omega_k
\tag{11}
$$
ここで
$$\boldsymbol{x_k} =
\begin{pmatrix}
\theta_k \\
\omega_{offset}
\end{pmatrix}
、
A_{\theta} =
\begin{pmatrix}
1 & -\delta t \\
0 & 1
\end{pmatrix}
、
B_{\theta} =
\begin{pmatrix}
\delta t \\
0
\end{pmatrix}
、
u_k = \omega_k
$$
とします。
また、$\omega_{offset}$については各時刻で直接観測できないため、観測方程式は以下のようになります。
$$\theta_k =
\begin{pmatrix}
1 & 0
\end{pmatrix}
\begin{pmatrix}
\theta_k \\
\omega_{offset}
\end{pmatrix}
\tag{12}
$$
ここで
$$y_k = \theta_k
、
C_{\theta} =
\begin{pmatrix}
1 & 0
\end{pmatrix}
$$
とします。
姿勢推定用のカルマンフィルタ
以下の手順を繰り返すことによって、各ステップにおけるロボットの姿勢$(\theta_k)$を求めることができます。
- カルマンゲインの導出
まず以下の式によりカルマンゲイン$(G_k)$を導出します。
$$G_k = P^{\prime}_k C_{\theta}^T (W + C_{\theta} P^{\prime}_k C_{\theta}^T)^{-1} \tag{13}$$
ここで$P^{\prime}_k$は前ステップで予測した共分散行列、$W$は観測雑音$\boldsymbol{w_k}$が従う共分散であり、エンコーダによって計算された姿勢の共分散を用います。
- 共分散行列の導出
続いて、カルマンゲイン$(G_k)$と、1ステップ前で求めた共分散行列の予測値$(P^{\prime}_k)$を用いて、共分散行列を導出します。ここで$P_k$は各ステップにおける状態$\boldsymbol{x_k}$が従う確率密度関数の共分散行列を表しています。
$$P_k = (I - G_k C_{\theta}) P^{\prime}_k \tag{14}$$
ここで$I$は単位行列です。
- $\boldsymbol{x}$の最大事後確率$(\hat{\boldsymbol{x_k}})$導出
測定値$\boldsymbol{y}$が定まった前提で、状態 $\boldsymbol{x}$が従う条件付き確率密度関数である$P_{X|Y}(\boldsymbol{x}|\boldsymbol{y})$が最大化する最大事後確率推定値$\hat{\boldsymbol{x_k}}$を導出します。
$$\hat{\boldsymbol{x_k}} = \boldsymbol{x^{\prime}_k} + G_k (\theta_k - C_{\theta} \boldsymbol{x^{\prime}_k}) \tag{15}$$
ここで求めた$\hat{\boldsymbol{x_k}}$が、このステップにおけるカルマンフィルタを用いた状態の推定値となります。
- 数理モデルによる次ステップ$(k+1)$の状態予測
現在の推定値$\hat{\boldsymbol{x_k}}$と$\boldsymbol{x_k}$が従う確率密度関数の共分散行列$P_k$について、数理モデルを用いて次のステップにおける値を予測します。次のステップではこの予測値と、次ステップの計測値を用いて状態を推定します。
$$P^{\prime}_{k + 1} = A_{\theta} P_k A_{\theta}^T + B_{\theta} U B_{\theta}^T \tag{16}$$
ここで$U$は入力雑音の共分散を表しており、ジャイロセンサから得られる角速度の分散を用います。
$$\boldsymbol{x^{\prime}_{k+1}} =A_{\theta} \hat{\boldsymbol{x_k}} + B_{\theta} \omega_k \tag{17}$$
まとめ
ロボットの状態を予測するためにカルマンフィルタを用いてセンサフュージョンをすることを考えました。
今回は姿勢推定用の状態方程式と観測方程式を考え、カルマンフィルタを紹介しました。次回は位置推定用の状態方程式と観測方程式を考えようと思います。


